Ran across this terrific observation in Wallace’s book on set theory and mathematics, and thought I’d share:

The trouble with college math classes – which classes consist almost entirely in the rhythmic ingestion and regurgitation of abstract information, and are paced in such a way as to maximize this reciprocal data-flow – is that their shear surface-level difficulty can fool us into thinking we really know something when all we really “know” is abstract formulas and rules for their deployment. Rarely do math classes ever tell us if a formula is truely significant, or why, or where it came from, or what was at stake.

David Foster Wallace at the Hammer Museum in Los Angeles, January 2006. 2006 CC BY-SA 3.0

And, of course, rarely do students think to ask – the formulas alone take so much work to “understand” (i.e., be able to solve problems correctly with), we often aren;t aware that we don’t understand them at all. That we end up not even knowing that we don’t know if the most incidious part of most math classes.

– David Foster Wallace, in Everything and More (section 2a)

In the previous post, we have seen how the number of questions needed to determine the number selected in the non-adaptive/”no feedback” situation is closely connected with the construction of “best possible” error-correcting codes. Let us look at some tables of specific values.

Odd :

Even :

Next, we tabulate some values of for different values of (see R. Hill, J. Karim, E. Berlekamp, “The solution of a problem of Ulam on searching with lies,” IEEE, 1998):

What is remarkable, I think, is that even if you are allowed to modify your questions adaptively, depending on the answer given, it won’t help you very much.

A group of mathematicians in Los Angeles have developed, in a series of papers, a systems of two partial differential equations, in time and space coordinates, which describe the risk of a criminal attack. Andrea Bertozzi, director of the Computational and Applied Math group in the UCLA Math Dept, has co-arthored many papers on the subject.

An introduction is at The Mathematics of Clumpy Crime.

Again, a disclaimer: I got this book free and I know (by numerous emails over the years), the author of this text. Second, this book was also helped by Minh Van Nyuyen who I also know (by email); Minh was a student of McAndrew when the book was being written. If memory serves, I first emailed the author after reading his fine book Introduction to Digital Image Processing with MATLAB, hoping someone would write a corresponding book using Sage or Octave. That never happened, but this book did, and students of cryptography, old and young, will be grateful for it.

This is a well-written book on cryptography, suitable as a textbook for an undergraduate or graduate course in the topic. It is also useful for someone who just wants a reference book on how to do cryptographic computations in Sage. (Sage is a free and open-source mathematical software system, available from http://www.sagemath.org.)Each chapter has an extensive set of exercises, as well as a glossary. The exercises are broken into four groups: Review Exercises, Beginning Exercises, Sage Exercises, and Further (or more advanced) Exercises. The text tries to be self-contained, with definitions and key ideas illustrated with examples, many of which are supported by corresponding Sage commands.

The chapters will be briefly summarized next.

The first chapter, Introduction to Cryptography, sketches basic ideas such as confidentiality, various types of attacks, cryptographic protocols, and computer security. Some simple ciphers are given as examples.

Basic Number Theory is chapter 2. It covers some basic mathematical definitions in elementary number theory, talks about some of the commonly used computations such as the Euclidean algorithm and modular exponentiation.
Also, primality testing is covered.

Chapter 3 is Classical Cryptosystems. This covers the Caesar cipher, the Vigenère cipher, the one-time pad, and several permutation ciphers and matrix ciphers.

The fourth chapter, Introduction to Information Theory, introduces entropy and uncertainty, and illustrates the notions by estimating the entropy of typical English language text.

Chapter 5, Public-Key Cryptosystems Based on Factoring, covers the RSA cryptosystem, Rabin’s cryptosystem and ends with a discussion on the Pollard rho method of factoring large integers.

Public-Key Cryptosystems Based on Logarithms and Knapsacks, the sixth chapter, covers the discrete logarithm problem, El Gamal’s cryptosystem, the Diffie-Hellman key exchange, and Knapsack cryptosystems.

Chapter 7, Digital Signatures, talks about the RSA signature scheme, Rabin digital signatures, and the El Gamal digital signature scheme.

The eighth chapter, Block Ciphers and the Data Encryption Standard, discusses Block ciphers, DES, and Feistel ciphers.

Chapter 9 is a review of finite fields.

The Advanced Encryption Standard is chapter 10. This chapter covers both the usual AES but also a simplified Rijndael cipher. Both of these are implemented in Sage and Sage examples illiustrate the computations.

Chapter 11 is on Hash Functions. Their security, construction, and uses are discussed.

Chapter 12 is on Elliptic Curve Cryptosystems.About half the chapter sketches background on elliptic curves. This is a very technical topic, but one which Sage has a great deal of computational functionality implemented. The rest of the chapter covers elliptic curve cryptosystems, elliptic curve signature schemes, and related topics.

Random Numbers and Stream Ciphers is chapter 13. It covers such topics as pseudo-random number generators, Stream ciphers, RC4, and the Blum-Goldwasser cryptosystem.

The last chapter is Advanced Applications and Protocols. It covers topics such as zero knowledge proofs,
digital cash and voting protocols.

There are two appendices: one is an introduction to the mathematical software system Sage and the other summarizes some more advanced aspects of computational number theory. The book also has a good index.

Title: Sage – beginner’s guide

Author: Craig Finch

Technical Reviewers: Dr David Kirkby and Minh Nyugen.

Publisher: Packt Publishing, Open Source series

Review

Complete disclosure: I received this book for free from the publisher, with only the promise to put a review on this blog. Also, I have worked with one of the book’s reviewers (Minh) on a few projects. However, I didn’t receive any other renumeration, don’t know the author of the text under review, and no one asked to pre-approve this review.

The book under review is a book on Sage, an open source mathematical software package started by William Stein, a mathematician at the University of Washington. It is very carefully written (either that, or very carefully reviewed by the Technical Reviewers!) and aimed, as the title suggests, at the beginner. However, it is assumed that the reader knows some undergraduate mathematics, say the level one obtains from getting an engineering degree. In fact, it has a bit of an applied slant with many examples from physics and engineering mathematics. This is a welcome contrast to the excellent Sage Tutorial (available free from the Sage website, http://www.sagemath.org) which has a more of a pure slant. It’s nice to see a publisher like Packt Publishing take the risk of publishing a book like this on an open source software program which already has free documentation (in pdf form).

There are 10 chapters and it’s about 350 pages. Although Sage of course has color plotting, all figures in this book are in black and white, so the reader really must try out the Sage code given in the book to get the full effect. Each chapter features many Time for action Sage code examples (also conveniently listed in the table of contents at the front of the book), followed by a What just happened? section explaining in detail (and without computer code) what the example did. These make the book more useful to the beginner as well as for someone wanting a quick reference for one of the examples. All these examples use the command-line version of Sage (typing your commands into a terminal window at a sage: prompt) but there are several sections explaining the GUI version of Sage (typing your commands into a Mathematica-like “notebook cell”) as well.

Here is a chapter-by-chapter summary:

The first chapter, What can you do with Sage?, is a survey of some of Sage‘s most commonly used capabilities. Examples such as solving a differential equations, plotting experimental data, and some simple example matrix computations are presented.

The second chapter is Installing Sage. This covers the steps you go though for a Mac OS, Windows, and Linux installation of Sage. Since this is scary for a number of users who are not very computer-savvy, it is nice an entire chapter is devoted to this.

The third chapter, Getting started with Sage, introduces the new Sage user to the user interface, basic Sage syntax, user-defined functions, and some of the available data types (such as strings and real number types). For example, the (black and white version of the) Sage plot of the sinc function,

     sage: f(x) = sin(x)/x
     sage: plot(f, x, xmin=-15, xmax = 15, thickness=2, color="red", legend_label="sinc")

is discussed, among many other things.

This motivates a more detailed introduction to Python, given in the next chapter.

Introducing Python and Sage, the fourth chapter, introduces syntax for Python lists, dictionaries, for loops, if-then statements, and also reading and writing to files. Sage is based on Python, a popular language used extensively in industry (at google among other places). This chapter introduces some very useful stuff, but is pretty basic if you know Python already.

The 5th chapter is Vectors, matrices and linear algebra, and you can guess what it is about. Sage has very wide functionality in linear algebra, with specialized packages for numerical computations for real and complex matrices, matrices over a finite field, or matrices having symbolic coefficients, such as functions of a variable x.

Sage‘s functionality in two-dimensional and three-dimensional plotting is described in the 6th chapter, Plotting with Sage. There is 3-d “live-view” (i.e., you can use the mouse to rotate a plot of a surface or solid in 3-space), histogram plots, as well as simpler plots using Sage‘s 2-d plotting package, matplotlib.

Chapter 7 is Making symbolic mathematics easy. Various topics are covered, from various calculus operations, such as limits, derivatives, integrals, and Laplace transforms, to exact
solutions to equations with variable coefficients, to infinite sums such as power series, to solving ordinary differential equations.

Solving problems numerically is the next chapter. This is the meat-and-potatoes for an applied mathematician. Sage includes many packages which have been developed to solve optimization problems, linear programming problems, numerical solutions of ordinary differential equations, numerical integration, and probability and statistics. These are introduced briefly in this chapter.

The 9th chapter is Learning advanced python programming. Here object-oriented programming is introduced by means of examples, and it is shown how Python handles errors and imports.

The last chapter Where to go from here discusses selected miscellaneous advanced topics.
Topics covered include: LaTeX, interactive plotting using the Sage notebook, as well as a fairly detailed example of analyzing colliding spheres in Sage from several different approaches.

The book has a very good index and, overall I believe is a very welcomed addition to the literature of Sage books.

Earth Viewed by Apollo 8.

A matroid M is specified by a set X of “points” and a collection B of “bases, where , satisfying certain conditions (see, for example, Oxley’s book, Matroid theory).

One way to construct a matroid, as it turns out, is to consider a matrix M with coefficients in a field F. The column vectors of M are indexed by the numbers . The collection B of subsets of J associated to the linearly independent column vectors of M of cardinality 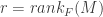forms a set of bases of a matroid having points .

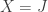How do you compute B? The following Sage code should work.

def independent_sets(mat):
    """
    Finds all independent sets in a vector matroid.

    EXAMPLES:
        sage: M = matrix(GF(2), [[1,0,0,1,1,0],[0,1,0,1,0,1],[0,0,1,0,1,1]])
        sage: M
        [1 0 0 1 1 0]
        [0 1 0 1 0 1]
        [0 0 1 0 1 1]
        sage: independent_sets(M)  
        [[0, 1, 2], [], [0], [1], [0, 1], [2], [0, 2], [1, 2], 
        [0, 1, 4], [4], [0, 4], [1, 4], [0, 1, 5], [5], [0, 5], 
        [1, 5], [0, 2, 3], [3], [0, 3], [2, 3], [0, 2, 5], [2, 5], 
        [0, 3, 4], [3, 4], [0, 3, 5], [3, 5], [0, 4, 5], [4, 5], 
        [1, 2, 3], [1, 3], [1, 2, 4], [2, 4], [1, 3, 4], [1, 3, 5], 
        [1, 4, 5], [2, 3, 4], [2, 3, 5], [2, 4, 5]]
        sage: M = matrix(GF(3), [[1,0,0,1,1,0],[0,1,0,1,0,1],[0,0,1,0,1,1]])
        sage: independent_sets(M)
        [[0, 1, 2], [], [0], [1], [0, 1], [2], [0, 2], [1, 2], 
        [0, 1, 4], [4], [0, 4], [1, 4], [0, 1, 5], [5], [0, 5], 
        [1, 5], [0, 2, 3], [3], [0, 3], [2, 3], [0, 2, 5], [2, 5], 
        [0, 3, 4], [3, 4], [0, 3, 5], [3, 5], [0, 4, 5], [4, 5], 
        [1, 2, 3], [1, 3], [1, 2, 4], [2, 4], [1, 3, 4], [1, 3, 5], 
        [1, 4, 5], [2, 3, 4], [2, 3, 5], [2, 4, 5], [3, 4, 5]]
        sage: M345 = matrix(GF(2), [[1,1,0],[1,0,1],[0,1,1]])
        sage: M345.rank()
        2
        sage: M345 = matrix(GF(3), [[1,1,0],[1,0,1],[0,1,1]])
        sage: M345.rank()
        3
    """
    F = mat.base_ring()
    n = len(mat.columns())
    k = len(mat.rows())
    J = Combinations(n,k)
    indE = []
    for x in J:
        M = matrix([mat.column(x[0]),mat.column(x[1]),mat.column(x[2])])
        if k == M.rank():     # all indep sets of max size
            indE.append(x)
            for y in powerset(x): # all smaller indep sets
                if not(y in indE):
                    indE.append(y)
    return indE

def bases(mat, invariant = False):
    """
    Find all bases in a vector/representable matroid.

    EXAMPLES:
        sage: M = matrix(GF(2), [[1,0,0,1,1,0],[0,1,0,1,0,1],[0,0,1,0,1,1]])
        sage: bases(M)

        [[0, 1, 2],
         [0, 1, 4],
         [0, 1, 5],
         [0, 2, 3],
         [0, 2, 5],
         [0, 3, 4],
         [0, 3, 5],
         [0, 4, 5],
         [1, 2, 3],
         [1, 2, 4],
         [1, 3, 4],
         [1, 3, 5],
         [1, 4, 5],
         [2, 3, 4],
         [2, 3, 5],
         [2, 4, 5]]
        sage: L = [x[1] for x in bases(M, invariant=True)]; L.sort(); L
         [5, 16, 17, 33, 37, 44, 45, 48, 81, 84, 92, 93, 96, 112, 113, 116]
    """
    r = mat.rank()
    ind = independent_sets(mat)
    B = []
    for x in ind:
        if len(x) == r:
            B.append(x)
    B.sort()
    if invariant == True:
        B = [(b,sum([k*2^(k-1) for k in b])) for b in B]
    return B

Let us assume that google’s basic philosophy is to make information free (see for example http://www.google.com/corporate/tenthings.html) This way they can increase the value of the internet and the value of their search technology.

What can Google do to help the problem of the inflation of academic journals? The fundamental issue is the disparity between the ease of communicating information (scientific information which is, by community consensus, free) and the relatively difficult implementation of the nature human desire to make money by selling access to that information. The basic economic model is that taxpayers are the primary support for academic research at a US class I or a European university (tuition actually only fund a minority share of the cost of running an academic institution). On the other hand, taxpayers also pay for the cost of these journals to these academic institutions. If you, a typical taxpayer, enjoy paying twice or getting double-billed, I have two bridges in Brooklyn I’d like sell you.

In case the typical taxpayer thinks this is an issue they can hide from, I warn you, some of these journals are not cheap (eg, some are on the order of a few thousand dollars per issue). Moreover, some publishers, such as Reed Elsevier not only charge a couple of grand per issue but also publishes bogus journals (see for example (http://laikaspoetnik.wordpress.com/2009/05/08/mercks-ghostwriters-haunted-papers-and-fake-elsevier-journals/) and pays for fake positive reviews (http://golem.ph.utexas.edu/category/2009/07/elsevier_pays_for_favorable_bo.html).

The solution to this dilemma is rather simple, Taxpayers must insist that their research dollars only fund research which is available for free. In other words, the results of the their funded research much be publicly available. This goes for papers and software supported by their funding.

As a matter of complete disclosure, some institutions now require that their faculty post their research papers on free web servers (for example MIT), and some funding agencies require taht thier grantees make available their grantees research papers available on such servers (for example, NIH in the US).

Can Google play a role here? I think so.

A colleague Bill Wardlaw (Robert Steinberg’s 2nd PhD student, I believe) retired recently and I was offered his office. I thought “this will be a nice chance to clean out all the junk I’ve accumulated” and started the move yesterday. You know those boxes that reams of xerox paper gets delivered in? I had 12 of those boxes filled with preprints, many unsorted – not counting the piles of papers which were on top of the boxes because I was too lazy to put them in. I resolved to throw away every paper I had not looked at in the past two years or I had a copy of electronically.

I started with a random box and managed to toss some papers out before running across an old, very well-worn xerox copy of Hejhal’s “Selberg’s trace formula and the Riemann zeta function” (published in the Duke Math J, but I forgot the year). I could not make myself throw it away! I had these intense memories of the times I loved reading it. In fact, I’ve read that paper several times and loved it each time. I realized I loved that paper too much to trash it. A little extreme since it was just a xerox copy but I just figured I’ll just save that one paper.

Back to work, I trashed several more papers and eventually came across some mimeographed notes of A. Weil, signed by Weil himself. I can’t throw away a piece of mathematical history! By the way, my memory of things is that I got these papers by being assigned Larry Goldstein’s old office at the University of Maryland (I was there for 1 year after graduating in 1983 and LG had just retired), who cleaned out his office but left a few old preprints assuming they would be trashed I guess. The reason LG had them was because he somehow inherited some papers of Robert Mountjoy. I remember hearing that RM died in a traffic accident on his way from Princeton, where he had a postdoc, to the University of Maryland, where he was going to start a tenure track job. I remember hearing that Mountjoy was a student of Andre Weil but according to the math genealogy project, he was a student of Saunders MacLane. In any case, he graduated from the University of Chicago in 1964 and Weil left Chicago for the IAS in 1958, so Weil could not have been his official advisor. Mountjoy got these papers from Weil himself. Now I have them and, to me, they are priceless. They remind me of the 2 times I met Prof Weil. One was a party given by V. Chari and the other was a dinner at an India restaurant with V. Chari, A. Weil and myself. Weil knew VC because he once spend some time in India where he became close friends with VC’s father. I remember he gave me the problem of trying to generalize his proof of quadratic reciprocity using Eisenstein series of the 2-fold metaplectic cover of SL(2) to prove higher reciprocity using n-fold covers. I never was able to solve his problem (I think it is still unsolved) but will never forget his kindness (nor VC’s, though she was young herself too at the time) towards a very young and very green postdoc. So, I cherish and treasure those preprints and could never throw them away either.

Are you starting to see the pattern? To make a long story short, I started with 12+ boxes and, at the end of the process, ended up with 7 boxes. There are too many papers I either love now or have strong memories of the time I enjoyed reading them. Some were just beautifully written, some full of extraordinary ideas, and some just astonishing for their display of shear mathematical wizardry.

I guess I’m a mathematical romantic.

There is a great post on this topic here:

http://trombonechamp.wordpress.com/2008/06/23/10-reasons-why-free-software-and-gnulinux-should-be-used-in-schools/