As in the previous post, let 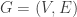be a weighted digraph having 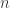vertices and let 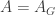denote its 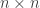adjacency matrix. We identify the vertices with the set .

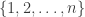The previous post discussed the following result, due to Sturmfels et al.

Theorem: The entry of the matrix A ^n-1 in row i and column j equals the length of a shortest path from vertex i to vertex j in G. (Here A ^n-1 denotes the n-1-st tropical power of A.)

This post discusses an implementation in Python/Sage.

Consider the following class definition.

class TropicalNumbers:
    """
    Implements the tropical semiring.

    EXAMPLES:
        sage: T = TropicalNumbers()
        sage: print T
        Tropical Semiring

    """
    def __init__(self):
        self.identity = Infinity

    def __repr__(self):
        """
        Called to compute the "official" string representation of an object.
        If at all possible, this should look like a valid Python expression
        that could be used to recreate an object with the same value.

        EXAMPLES:
            sage: TropicalNumbers()
            TropicalNumbers()

        """
        return "TropicalNumbers()"

    def __str__(self):
        """
        Called to compute the "informal" string description of an object. 

        EXAMPLES:
            sage: T = TropicalNumbers()
            sage: print T
            Tropical Semiring

        """
        return "Tropical Semiring"

    def __call__(self, a):
        """
        Coerces a into the tropical semiring.

        EXAMPLES:
            sage: T(10)
            TropicalNumber(10)
            sage: print T(10)
            Tropical element 10 in Tropical Semiring
        """
        return TropicalNumber(a)

    def __contains__(self, a):
        """
        Implements "in".

        EXAMPLES:
            sage: T = TropicalNumbers()
            sage: a = T(10)
            sage: a in T
            True

        """
        if a in RR or a == Infinity:
            return a==Infinity or (RR(a) in RR)
        else:
            return a==Infinity or (RR(a.element) in RR)

class TropicalNumber:
    def __init__(self, a):
        self.element = a
        self.base_ring = TropicalNumbers()

    def __repr__(self):
        """
        Called to compute the "official" string representation of an object.
        If at all possible, this should look like a valid Python expression
        that could be used to recreate an object with the same value.

        EXAMPLES:

        """
        return "TropicalNumber(%s)"%self.element

    def __str__(self):
        """
        Called to compute the "informal" string description of an object. 

        EXAMPLES:
            sage: T = TropicalNumbers()
            sage: print T(10)
            Tropical element 10 in Tropical Semiring
        """
        return "%s"%(self.number())

    def number(self):
        return self.element

    def __add__(self, other):
        """
        Implements +. Assumes both self and other are instances of
        TropicalNumber class.

        EXAMPLES:
            sage: T = TropicalNumbers()
            sage: a = T(10)
            sage: a in T
            True
            sage: b = T(15)
            sage: a+b
            10

        """
        T = TropicalNumbers()
        return T(min(self.element,other.element))

    def __mul__(self, other):
        """
        Implements multiplication *.

        EXAMPLES:
            sage: T = TropicalNumbers()
            sage: a = T(10)
            sage: a in T
            True
            sage: b = T(15)
            sage: a*b
            25
        """
        T = TropicalNumbers()
        return T(self.element+other.element)

class TropicalMatrix:
    def __init__(self, A):
        T = TropicalNumbers()
        self.base_ring = T
        self.row_dimen = len(A)
        self.column_dimen = len(A[0])
        # now we coerce the entries into T
        A0 = A
        m = self.row_dimen
        n = self.column_dimen
        for i in range(m):
            for j in range(n):
                A0[i][j] = T(A[i][j])
        self.array = A0

    def matrix(self):
        """
        Returns the entries (as ordinary numbers).

        EXAMPLES:
            sage: A = [[0,1,3,7],[2,0,1,3],[4,5,0,1],[6,3,1,0]]
            sage: AT = TropicalMatrix(A)
            sage: AT.matrix()
            [[0, 1, 3, 7], [2, 0, 1, 3], [4, 5, 0, 1], [6, 3, 1, 0]]
        """
        m = self.row_dim()
        n = self.column_dim()
        A0 = [[0 for i in range(n)] for j in range(m)]
        for i in range(m):
            for j in range(n):
                A0[i][j] = (self.array[i][j]).number()
        return A0

    def row_dim(self):
        return self.row_dimen

    def column_dim(self):
        return self.column_dimen

    def __repr__(self):
        """
        Called to compute the "official" string representation of an object.
        If at all possible, this should look like a valid Python expression
        that could be used to recreate an object with the same value.

        EXAMPLES:

        """
        return "TropicalMatrix(%s)"%self.array

    def __str__(self):
        """
        Called to compute the "informal" string description of an object. 

        EXAMPLES:

        """
        return "Tropical matrix %s"%(self.matrix())

    def __add__(self, other):
        """
        Implements +. Assumes both self and other are instances of
        TropicalMatrix class.

        EXAMPLES:
            sage: A = [[1,2,Infinity],[3,Infinity,0]]
            sage: B = [[2,Infinity,1],[3,-1,1]]
            sage: AT = TropicalMatrix(A)
            sage: BT = TropicalMatrix(B)
            sage: AT
            TropicalMatrix([[TropicalNumber(1), TropicalNumber(2), TropicalNumber(+Infinity)],
              [TropicalNumber(3), TropicalNumber(+Infinity), TropicalNumber(0)]])
            sage: AT+BT
            [[TropicalNumber(1), TropicalNumber(2), TropicalNumber(1)],
             [TropicalNumber(3), TropicalNumber(-1), TropicalNumber(0)]]
        """
        A = self.array
        B = other.array
        C = []
        m = self.row_dim()
        n = self.column_dim()
        if m != other.row_dim:
            raise ValueError, "Row dimensions must be equal."
        if n != other.column_dim:
            raise ValueError, "Column dimensions must be equal."
        for i in range(m):
            row = [A[i][j]+B[i][j] for j in range(n)] # + as tropical numbers
            C.append(row)
        return C

    def __mul__(self, other):
        """
        Implements multiplication *.

        EXAMPLES:
            sage: A = [[1,2,Infinity],[3,Infinity,0]]
            sage: AT = TropicalMatrix(A)
            sage: B = [[2,Infinity],[-1,1],[Infinity,0]]
            sage: BT = TropicalMatrix(B)
            sage: AT*BT
             [[TropicalNumber(1), TropicalNumber(3)],
              [TropicalNumber(5), TropicalNumber(0)]]
            sage: A = [[0,1,3,7],[2,0,1,3],[4,5,0,1],[6,3,1,0]]
            sage: AT = TropicalMatrix(A)
            sage: A = [[0,1,3,7],[2,0,1,3],[4,5,0,1],[6,3,1,0]]
            sage: AT = TropicalMatrix(A)
            sage: print AT*AT*AT
            Tropical matrix [[0, 1, 2, 3], [2, 0, 1, 2], [4, 4, 0, 1], [5, 3, 1, 0]]
        """
        T = TropicalNumbers()
        A = self.matrix()
        B = other.matrix()
        C = []
        mA = self.row_dim()
        nA = self.column_dim()
        mB = other.row_dim()
        nB = other.column_dim()
        if nA != mB:
            raise ValueError, "Column dimension of A and row dimension of B must be equal."
        for i in range(mA):
            row = []
            for j in range(nB):
                c = T(Infinity)
                for k in range(nA):
                    c = c+T(A[i][k])*T(B[k][j])
                row.append(c.number())
            C.append(row)
        return TropicalMatrix(C)

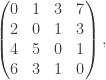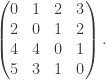This shows that the shortest distances of digraph with adjacency matrix is equal to A ³, which is equal to This verifies an example given in chapter 1 of the book by Maclagan and Sturmfels, Introduction to Tropical Geometry .