Simple unsolved math problem, 4

Posted on 2016/11/23 by wdjoyner

Problem: Optimally pack n unit circles into the smallest possible equilateral triangle.

circle-packing_60_60_60_wikipedia

Let L(n) denote the length of the side of the smallest equilateral triangle in which n circles have been packed optimally. This number is, in general, unknown.

The minimum upset ranking problem

Posted on 2016/11/11 by wdjoyner

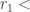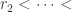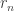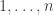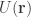Suppose n teams play each other, and let Team $r_1 <$ Team $r_2 < \dots <$ Team $r_n$ denote some fixed ranking (where $r_1,\dots,r_n$ is some permutation of $1,\dots,n$ ). An upset occurs when a lower ranked team beats an upper ranked team. For each ranking, ${\bf r}$ , let $U({\bf r})$ denote the total number of upsets. The minimum upset problem is to find an “efficient” construction of a ranking for which 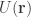$U({\bf r})$ is as small as possible.

In general, let $A_{ij}$ denote the number of times Team i beat team $j$ minus the number of times Team j beat Team i. We regard this matrix as the signed adjacency matrix of a digraph $\Gamma$ . Our goal is to find a Hamiltonian (undirected) path through the vertices of $\Gamma$ which goes the “wrong way” on as few edges as possible.

Construct the list of spanning trees of $\Gamma$ (regarded as an undirected graph).
Construct the sublist of Hamiltonian paths (from the spanning trees of maximum degree 2).
For each Hamiltonian path, compute the associated upset number: the total number of edges transversal in $\Gamma$ going the “right way” minus the total number going the “wrong way.”
Locate a Hamiltonian for which this upset number is as large as possible.

Use this sagemath/python code to compute such a Hamiltonian path.

def hamiltonian_paths(Gamma, signed_adjacency_matrix = []):
    """
    Returns a list of hamiltonian paths (spanning trees of 
    max degree <=2).

    EXAMPLES:
        sage: Gamma = graphs.GridGraph([3,3])
        sage: HP = hamiltonian_paths(Gamma)
        sage: len(HP)
        20
        sage: A = matrix(QQ,[
        [0 , -1 , 1  , -1 , -1 , -1 ],
        [1,   0 ,  -1,  1,  1,   -1  ],
        [-1 , 1 ,  0 ,  1 , 1  , -1  ],
        [1 , -1 , -1,  0 ,  -1 , -1  ],
        [1 , - 1 , - 1 , 1 , 0 , - 1  ],
        [1 ,  1  ,  1  , 1  , 1  , 0 ]
        ])
        sage: Gamma = Graph(A, format='weighted_adjacency_matrix')
        sage: HP = hamiltonian_paths(Gamma, signed_adjacency_matrix = A)
        sage: L = [sum(x[2]) for x in HP]; max(L)
        5
        sage: L.index(5)
        21
        sage: HP[21]                                 
        [Graph on 6 vertices,
         [0, 5, 2, 1, 3, 4],
         [-1, 1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, 1, 1, -1]]
        sage: L.count(5)
        1

    """
    ST = Gamma.spanning_trees()
    if signed_adjacency_matrix == []:
        HP = []
        for X in ST:
            L = X.degree_sequence()
            if max(L)<=2:
                #print L,ST.index(X), max(L)
                HP.append(X)
        return HP
    if signed_adjacency_matrix != []:
        A = signed_adjacency_matrix
        HP = []
        for X in ST:
            L = X.degree_sequence()
            if max(L)<=2:
                #VX = X.vertices()
                EX = X.edges()
		if EX[0][1] != EX[-1][1]:
                    ranking = X.shortest_path(EX[0][0],EX[-1][1])
		else:
		    ranking = X.shortest_path(EX[0][0],EX[-1][0])
		signature = [A[ranking[i]][ranking[j]] for i in range(len(ranking)-1) for j in range(i+1,len(ranking))]
                HP.append([X,ranking,signature])
        return HP

Wessell describes this method in a different way.

Construct a matrix, $M=(M_{ij})$ , with rows and columns indexed by the teams in some fixed order. The entry in the i-th row and the j-th column is defined by $m_{ij}= \left\{ \begin{array}{rr} 0,& {\rm if\ team\ } i {\rm \ lost\ to\ team\ } j,\\ 1,& {\rm if\ team\ } i {\rm\ beat\ team\ } j,\\ 0, & {\rm if}\ i=j. \end{array} \right.$
Reorder the rows (and corresponding columns) to in a basic win-loss order: the teams that won the most games go at the
top of $M$ , and those that lost the most at the bottom.
Randomly swap rows and their associated columns, each time checking if the
number of upsets has gone down or not from the previous time. If it has gone down, we keep
the swap that just happened, if not we switch the two rows and columns back and try again.

An implementaiton of this in Sagemath/python code is:

def minimum_upset_random(M,N=10):
    """
    EXAMPLES:
        sage: M = matrix(QQ,[
        [0 , 0 , 1  , 0 , 0 , 0 ],
        [1,   0 ,  0,  1,  1,   0  ],
        [0 , 1 ,  0 ,  1 , 1  , 0  ],
        [1 , 0 , 0,  0 ,  0 , 0  ],
        [1 , 0 , 0 , 1 , 0 , 0  ],
        [1 ,  1  ,  1  , 1  , 1  , 0 ]
        ])
        sage: minimum_upset_random(M)
        (
        [0 0 1 1 0 1]                    
        [1 0 0 1 0 1]                    
        [0 1 0 0 0 0]                    
        [0 0 1 0 0 0]                    
        [1 1 1 1 0 1]                    
        [0 0 1 1 0 0], [1, 2, 0, 3, 5, 4]
        )

    """
    n = len(M.rows())
    Sn = SymmetricGroup(n)
    M1 = M
    wins = sum([sum([M1[j][i] for i in range(j,6)]) for j in range(6)])
    g0 = Sn(1)
    for k in range(N):
        g = Sn.random_element()
        P = g.matrix()
        M0 = P*M1*P^(-1)
        if sum([sum([M0[j][i] for i in range(j,6)]) for j in range(6)])>wins:
            M1 = M0
            g0 = g*g0
    return M1,g0(range(n))

Simple unsolved math problem, 3

Posted on 2016/10/22 by wdjoyner

A perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself. For example, 1 + 2 + 3 = 6 implies 6 is a perfect number.

Unsolved Problem: Are there any odd perfect numbers?

The belief, by some, that there are none goes back over 500 years (wikipedia).

If you want to check out some recent research into this problem, see oddperfect.org.

b5527a1273f40d19e7fa821caa0208b9

(Another unsolved problem: Are there an infinite number of even perfect numbers?)

Simple unsolved math problem, 2

Posted on 2016/10/18 by wdjoyner

In 1911, Otto Toeplitz asked the following question.

Inscribed Square Problem: Does every plane simple closed curve contain all four vertices of some square?

This question, also known as the square peg problem or the Toeplitz’ conjecture, is still unsolved in general. (It is known in lots of special cases.)

Inscribed square, by Claudio Rocchini

Thanks to Mark Meyerson (“Equilateral triangles and continuous curves”,Fundamenta Mathematicae, 1980) and others, the analog for triangles is true. For any triangle T and Jordan curve C, there is a triangle similar to T and inscribed in C. (In particular, the triangle can be equilateral.) The survey page by Mark J. Nielsen has more information on this problem.

Added 2016-11-23: See also this recent post by T. Tao.

Added 2020-07-01: This has apparently been solved by Joshua Greene and Andrew Lobb! See their ArXiV paper (https://arxiv.org/abs/2005.09193).

Simple unsolved math problem, 1

Posted on 2016/10/16 by wdjoyner

In 1937 Lothar Collatz proposed the 3n+1 conjecture (known by a long list of aliases), is stated as follows.

First, we define the function $f$ on the set of positive integers:

If the number $n$ is even, divide it by two: $f(n)=n/2$ .
If the number $n$ is odd, triple it and add one: $f(n)=3n+1$ .

In modular arithmetic notation, define the function $f$ as follows:
$f(n)= {n/2},\ if \ n\equiv 0 \pmod 2$ , and $f(n)= {3n+1},\ if \ n\equiv 1 \pmod 2$ . Believe it or not, this is the restriction to the positive integers of the complex-valued map $(2+7z-(2+5z)\cos(\pi z))/4$ .

The 3n+1 conjecture is: The sequence
$n,\ f(n),\ f^2(n)=f(f(n)),\ f^3(n)=f(f^2(n)),\ \dots$
will eventually reach the number 1, regardless of which positive integer $n$ is chosen initially.

This is still unsolved, though a lot of people have worked on it. For a recent survey of results, see the paper by Chamberland.

From xkdc by Randall Munroe – https://xkcd.com/710/

Problem of the week, 161

Posted on 2016/09/24 by wdjoyner

A former colleague Bill Wardlaw (March 3, 1936-January 2, 2013) used to create a “Problem of the Week” for his US Naval Academy students, giving a prize of a cookie if they could solve it. One of them is given below.

The residue of an integer n modulo an integer d > 1 is the remainder r left when n is divided by d. That is, if n = dq + r for integers q and r with 0 < r < d, we write $r \equiv n \pmod d$ for the residue of n modulo d. Show that the residue modulo 7 of a (large) integer n can be found by separating the integer into 3-digit blocks $n = b(s)b(s-1)\dots b(1)$ .(Note that b(s) may have 1, 2, or 3 digits, but every other block must have exactly three digits.) Then the residue modulo 7 of n is the same as the residue modulo 7 of $b(1) - b(2) + b(3) - b(4) + \dots \pm b(s)$ . For example,
$n = 25,379,885,124,961,154,398,521,655 \pmod 7$
$\equiv 655 - 521 + 398 - 154 + 961 - 124 + 885 - 379 + 25 \pmod 7$ $\equiv 1746 \pmod 7$ $\equiv 746 - 1 \pmod 7$ $\equiv 745 \pmod 7 \equiv 3 \pmod 7$ .
Explain why this works and show that the same trick works for residues modulo 13.

Problem of the week, 137

Posted on 2016/09/18 by wdjoyner

Chain addition is a technique employed in cryptography for extending a short sequence of digits, called the seed to a longer sequence of pseudorandom digits. Quoting David Kahn (in Kahn on Codes, MacMillan, New York, 1983, p. 154), “the first two digits of the [seed] are added together modulo 10 [which means they are added and the carry is neglected] and the result placed at the end of the [sequence], then the second and third digits are added and the sum placed at the end, and so forth, using also the newly generated digits when the [seed] is exhausted, until the desired length is obtained”. Thus, the seed 3964 yields the sequence 3964250675632195… .

Periodic pattern

a. Show that this sequence eventually repeats itself.
b. Show that the sequence begins repeating itself with “3964”.
c. EXTRA CREDIT: How many digits are there before the first repetition of “3964”?

Problem of the week, 148

Posted on 2016/09/17 by wdjoyner

Suppose p and q are each monic polynomials of degree 4 with real coefficients and the intersection of their graphs is {(1, 3), (5, 21)}. If p(3) – q(3) = 20, what is the area enclosed by their graphs?

Problem of the week, 150

Posted on 2016/09/17 by wdjoyner

Let a, b, and c be real numbers and let f and g be real valued functions of a real variable such that $\lim_{x\to a} g(x) = b$ and $\lim_{x\to b} f(x) = c$ .
a. Give an example in which $\lim_{x\to a} f(g(x)) \not= c$ .
b. Give an additional condition on f alone and show that it
guarantees $\lim_{x\to a} f(g(x)) = c$ .
c. Give an additional condition on g alone and show that it
guarantees $\lim_{x\to a} f(g(x)) = c$ .

Odd king tours on even chessboards

Posted on 2016/09/08 by wdjoyner

This blog post discusses a paper “Odd king tours …” written with Michael Fourte (a CS undergrad at the time, now is a lawyer and Naval officer in NYC) in 1997. It was published in the now defunct Journal of Recreational Mathematics, issue 31(3), in 2003.

In the paper, we showed that there is no complete odd king tour on an even chessboard, partially answering a question raised in [BK], [S]. This post surveys that paper.

King moves on an 8×8 board.

A complete king tour on an $m\times n$ board may be represented graph theoretically as a Hamiltonian cycle on a particular graph with $mn$ vertices, of which $(m-2)\cdot (n-2)$ of them have degree $8$ , $2(m+n-4)$ have degree $5$ and the remaining $4$ vertices have degree $3$ . The problem of finding an algorithm to find a hamiltonian circuit in a general graph is known to be NP complete. The problem of finding an efficient algorithm to search for such a tour therefore appears to be very hard problem. In [BK], C. Bailey and M. Kidwell proved that complete even king tours do not exist. They left the question of the existence of complete odd tours open but showed that if they did exist then it would have to end at the edge of the board.

We shall show that
Theorem: No complete odd king tours exist on an $m\times n$ board, except possibly in the following cases:

$m=n=7$
$m=7$ and $n=8$ ,
$m >7$ , $n >7$ and $m$ or $n$ (or both) is odd,
$m>7$ , $n>7$ and the tour is “rapidly filling”.

The definition of “rapidly filling” requires some technical notation and will be given later.

Background

Before proving this, we recall briefly some definitions and results from [BK] which we shall use in our proof.

Definition: Two squares are called a neighbor pair if they have a common edge or common vertex. A neighbor pair is called completed if both squares have been visited by the the king at some point in a tour, including the case where the king is still on one of the squares. A foursome is a collection of four squares which form a $2\times 2$ array of neighboring squares on the board. A foursome is called completed if all four squares have been visited by the the king at some point in a tour, including the case where the king is still on one of the four squares.

Unless stated otherwise, after a given move of a given odd king tour, let $\Delta F$ denote the change in the number of completed foursomes and let $\Delta N$ denote the change in the number of completed neighbor pairs. Note that $\Delta N$ is equal to the total number of previously visited squares which are neighboring the king.

The following result was proven in [BK] using a counting argument.

Lemma:

The number of neighbor pairs of an $m\times n$ board is $2mn+2(m-1)(n-1)-m-n.$
(b) The number of foursomes of an $m\times n$ board is $(m-1)(n-1).$

The following result was proven in [BK] using a case-by-case argument:

Lemma: After a particular move in a given even king tour, let $\Delta F$ denote the change in the number of completed foursomes and let $\Delta N$ denote the change in the number of completed neighbor pairs. If $\Delta F=0$ then $\Delta N\geq 2$ . If $\Delta F=1$ then $\Delta N\geq 4$ . If $\Delta F=2$ then $\Delta N\geq 6$ . If $\Delta F=3$ then $\Delta N =8$ .

We shall need the proof of this lemma (for which we refer the reader to [BK]) rather than the lemma itself. The proof of this lemma implies the following:

Lemma: For an odd king tour: If $\Delta F=0$ then $Delta N\geq 1$ . If $\Delta F=1$ then $\Delta N \geq 3$ . If $\Delta F=2$ then $\Delta N\geq 5$ . If $\Delta F=3$ then $\Delta N =7$ .

The proof is omitted.

Definition: We call an odd king tour rapidly filling if there is a move in the tour such that $2\Delta F +1<\Delta N$ and $1\leq \Delta F$ .

The proof of the theorem

Proposition: If $m$ and $n$ are both even then no complete odd king tour exists.

proof: Let $N$ denote the total number of completed neighbor pairs after a given point of a given odd king tour. We may represent the values of $N$ as a sequence of numbers, $0,1,2,...$ . Here $0$ is the total number of completed neighbor pairs after the first move, $1$ for after the second move, and so on. Each time the king moves, $N$ must increase by an odd number of neighbors – either $1$ , $3$ , $5$ , or $7$ . In particular, the parity of $N$ alternates between odd and even after every move. If $m$ and $n$ are both even and if a complete odd king tour exists then the the final parity of $N$ must be odd. By the lemma above, the value of $N$ after any complete king tour is $2mn+2(m-1)(n-1)-m-n$ , which is obviously even. This is a contradiction. QED

It therefore suffices to prove the above theorem in the case where at least one of $m,n$ is odd. This follows from a computer computation, an argument from Sands [Sa], and the sequence of lemmas that follow. The proofs are in the original paper, and omitted.

Let $N$ denote the total number of completed neighbor pairs in a given odd king tour. Let $F$ denote the number of completed foursomes in a given odd king tour. Let $M$ denote the number of moves in a given odd king tour. Let $T=N-2M-2F+4.$

Lemma: Let $\Delta T=\Delta N - 2 - 2\Delta F$ , where $\Delta N ,\Delta F$ are defined as above. Then $\Delta T$ equals $-1$ , $1$ , $3$ , or $5$ . If the tour is not rapidly filling then $\Delta T\geq 1$ only occurs when $\Delta F= 0$ .

Lemma: Let $H(m,n)$ denote the largest number of non-overlapping $2\times 2$ blocks which will fit in the $m\times n$ board. There are no labelings of the $m\times n$ checkerboard by $0$ ‘s and $1$ ‘s with no $2\times 2$ blocks of $1$ ‘s and fewer than $H(m,n)$ $0$ ‘s. In particular, if there are no $2\times 2$ blocks of 1’s then there must be at least $[m/2][n/2]$ 0’s.

We conclude with a question. An odd king tour of length $mn-1$ on an $m\times n$ board will be called nearly complete. Which boards have nearly complete odd king tours? We conjecture: If $n >$ then all $7\times n$ boards have nearly complete odd king tours.

References

[BK] C. Bailey, M. Kidwell, “A king’s tour of the chessboard”, Math. Mag. 58(1985)285-286

[S] S. Sacks, “odd and even”, Games 6(1982)53.

[Sa] B. Sands, “The gunport problem”, Math. Mag. 44(1971)193-194.