An experimental post

I asked Gemini to create a blog post based on this plot (below) and the Python code I wrote (based on ideas explained to me by Edray Goins) that generated it. (The prompt I fed to Gemini was modified from a prompt found online for generating a blog post about food.) The response, basically unedited, is below. The topic is inspired by the PhD thesis of Euphemia Haynes (a student of Aubrey Landry, Catholic University of America, 1943). See this earlier post for more information on it.

Mathematics can be beautiful, and sometimes that beauty is hidden in plain sight. Take, for instance, this striking image:

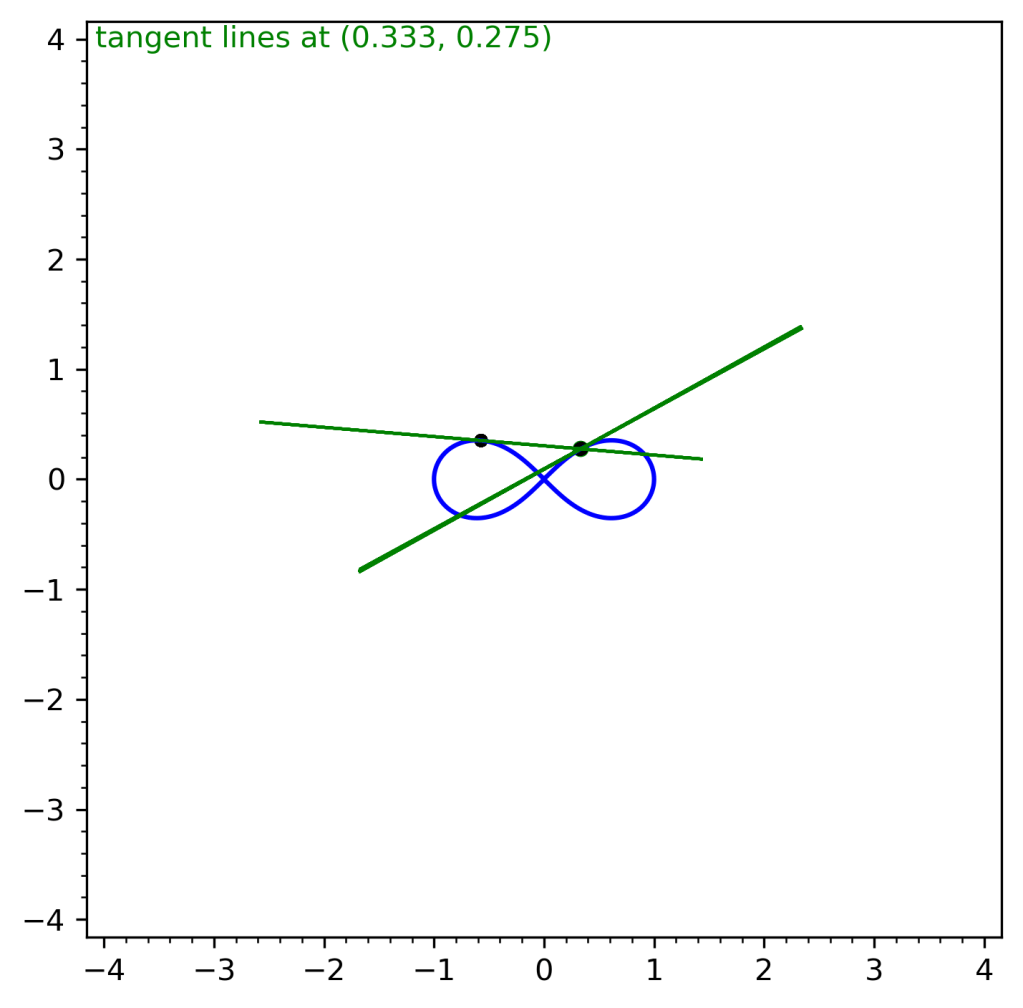
a graceful lemniscate curve adorned with a web of tangent lines, all seemingly converging on a single point. This isn’t some artistic rendering; it’s the output of a fascinating algorithm, written in Python and SageMath, plot_lemniscate_quartic_tangents.

This algorithm doesn’t just draw a pretty picture; it solves a sophisticated geometric problem: finding all the tangent lines to a lemniscate quartic that also pass through a specific point on the curve. Let’s dissect the magic:

1. The Lemniscate: The algorithm begins by defining the lemniscate quartic curve. This curve, shaped like a sideways figure-eight, has a unique and elegant equation: (x² + y²)² = a(x² – y²), where ‘a’ is a constant.
2. The Target Point: We choose a specific point, P0, on the lemniscate. This is the point where all our tangent lines will magically meet.
3. The Tangent Hunt: This is where the algorithm gets clever. It doesn’t directly solve for the tangent lines. Instead, it cleverly iterates through numerous points (P) on the lemniscate. For each point, it calculates two things:
   • The slope of the secant line connecting P0 and P.
   • The slope of the tangent line to the lemniscate at point P.
4. The Convergence: If the slopes from step 3 are approximately equal (within a tolerance), it means the secant line through P0 and P is also a tangent line to the curve at P. This line is added to our collection of tangent lines.
5. The Reveal: Finally, the algorithm plots the lemniscate along with all the tangent lines it discovered. The result is the captivating image we see—a testament to the hidden geometric relationships within this seemingly simple curve.

The algorithm isn’t just about finding tangents; it reveals a beautiful correspondence between points on the lemniscate and its tangent lines. It’s a visual exploration of the intricate geometry underlying algebraic curves, demonstrating how computation can unveil hidden mathematical beauty. So next time you see a seemingly simple curve, remember the rich and sometimes surprising geometry hiding within.