Let f be a Boolean function on  . The Cayley graph of f is defined to be the graph
. The Cayley graph of f is defined to be the graph
 ,
,
whose vertex set is  and the set of edges is defined by
and the set of edges is defined by
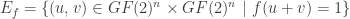 .
.
The adjacency matrix 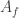 is the matrix whose entries are
is the matrix whose entries are
 ,
,
where b(k) is the binary representation of the integer k.
Note  is a regular graph of degree wt(f), where wt denotes the Hamming weight of f when regarded as a vector of values (of length
is a regular graph of degree wt(f), where wt denotes the Hamming weight of f when regarded as a vector of values (of length 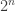 ).
).
Recall that, given a graph  and its adjacency matrix A, the spectrum Spec(
and its adjacency matrix A, the spectrum Spec( ) is the multi-set of eigenvalues of A.
) is the multi-set of eigenvalues of A.
The Walsh transform of a Boolean function f is an integer-valued function over  that can be defined as
that can be defined as

A Boolean function f is bent if 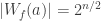 (this only makes sense if n is even). The Hadamard transform of a integer-valued function f is an integer-valued function over
(this only makes sense if n is even). The Hadamard transform of a integer-valued function f is an integer-valued function over  that can be defined as
that can be defined as

It turns out that the spectrum of  is equal to the Hadamard transform of f when regarded as a vector of (integer) 0,1-values. (This nice fact seems to have first appeared in [2], [3].)
is equal to the Hadamard transform of f when regarded as a vector of (integer) 0,1-values. (This nice fact seems to have first appeared in [2], [3].)
A graph is regular of degree r (or r-regular) if every vertex has degree r (number of edges incident to it). We say that an r-regular graph  is a strongly regular graph with parameters (v, r, d, e) (for nonnegative integers e, d) provided, for all vertices u, v the number of vertices adjacent to both u, v is equal to
is a strongly regular graph with parameters (v, r, d, e) (for nonnegative integers e, d) provided, for all vertices u, v the number of vertices adjacent to both u, v is equal to
e, if u, v are adjacent,
d, if u, v are nonadjacent.
It turns out tht f is bent iff  is strongly regular and e = d (see [3] and [4]).
is strongly regular and e = d (see [3] and [4]).
The following Sage computations illustrate these and other theorems in [1], [2], [3], [4].
Consider the Boolean function  given by
given by  .
.
sage: V = GF(2)^4
sage: f = lambda x: x[0]*x[1]+x[2]*x[3]
sage: CartesianProduct(range(16), range(16))
Cartesian product of [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15],
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15]
sage: C = CartesianProduct(range(16), range(16))
sage: Vlist = V.list()
sage: E = [(x[0],x[1]) for x in C if f(Vlist[x[0]]+Vlist[x[1]])==1]
sage: len(E)
96
sage: E = Set([Set(s) for s in E])
sage: E = [tuple(s) for s in E]
sage: Gamma = Graph(E)
sage: Gamma
Graph on 16 vertices
sage: VG = Gamma.vertices()
sage: L1 = []
sage: L2 = []
sage: for v1 in VG:
....: for v2 in VG:
....: N1 = Gamma.neighbors(v1)
....: N2 = Gamma.neighbors(v2)
....: if v1 in N2:
....: L1 = L1+[len([x for x in N1 if x in N2])]
....: if not(v1 in N2) and v1!=v2:
....: L2 = L2+[len([x for x in N1 if x in N2])]
....:
....:
sage: L1; L2
[2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]
[2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2,
2, 2, 2, 2]
This implies the graph is strongly regular with d=e=2.
sage: Gamma.spectrum()
[6, 2, 2, 2, 2, 2, 2, -2, -2, -2, -2, -2, -2, -2, -2, -2]
sage: [walsh_transform(f, a) for a in V]
[4, 4, 4, -4, 4, 4, 4, -4, 4, 4, 4, -4, -4, -4, -4, 4]
sage: Omega_f = [v for v in V if f(v)==1]
sage: len(Omega_f)
6
sage: Gamma.is_bipartite()
False
sage: Gamma.is_hamiltonian()
True
sage: Gamma.is_planar()
False
sage: Gamma.is_regular()
True
sage: Gamma.is_eulerian()
True
sage: Gamma.is_connected()
True
sage: Gamma.is_triangle_free()
False
sage: Gamma.diameter()
2
sage: Gamma.degree_sequence()
[6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6, 6]
sage: show(Gamma)
# bent-fcns-cayley-graphs1.png
Here is the picture of the graph:

sage: H = matrix(QQ, 16, 16, [(-1)^(Vlist[x[0]]).dot_product(Vlist[x[1]]) for x in C])
sage: H
[ 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
[ 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1 1 -1]
[ 1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 1 1 -1 -1]
[ 1 -1 -1 1 1 -1 -1 1 1 -1 -1 1 1 -1 -1 1]
[ 1 1 1 1 -1 -1 -1 -1 1 1 1 1 -1 -1 -1 -1]
[ 1 -1 1 -1 -1 1 -1 1 1 -1 1 -1 -1 1 -1 1]
[ 1 1 -1 -1 -1 -1 1 1 1 1 -1 -1 -1 -1 1 1]
[ 1 -1 -1 1 -1 1 1 -1 1 -1 -1 1 -1 1 1 -1]
[ 1 1 1 1 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1]
[ 1 -1 1 -1 1 -1 1 -1 -1 1 -1 1 -1 1 -1 1]
[ 1 1 -1 -1 1 1 -1 -1 -1 -1 1 1 -1 -1 1 1]
[ 1 -1 -1 1 1 -1 -1 1 -1 1 1 -1 -1 1 1 -1]
[ 1 1 1 1 -1 -1 -1 -1 -1 -1 -1 -1 1 1 1 1]
[ 1 -1 1 -1 -1 1 -1 1 -1 1 -1 1 1 -1 1 -1]
[ 1 1 -1 -1 -1 -1 1 1 -1 -1 1 1 1 1 -1 -1]
[ 1 -1 -1 1 -1 1 1 -1 -1 1 1 -1 1 -1 -1 1]
sage: flist = vector(QQ, [int(f(v)) for v in V])
sage: H*flist
(6, -2, -2, 2, -2, -2, -2, 2, -2, -2, -2, 2, 2, 2, 2, -2)
sage: A = matrix(QQ, 16, 16, [f(Vlist[x[0]]+Vlist[x[1]]) for x in C])
sage: A.eigenvalues()
[6, 2, 2, 2, 2, 2, 2, -2, -2, -2, -2, -2, -2, -2, -2, -2]
Here is another example:  given by
given by 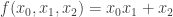 .
.
sage: V = GF(2)^3
sage: f = lambda x: x[0]*x[1]+x[2]
sage: Omega_f = [v for v in V if f(v)==1]
sage: len(Omega_f)
4
sage: C = CartesianProduct(range(8), range(8))
sage: Vlist = V.list()
sage: E = [(x[0],x[1]) for x in C if f(Vlist[x[0]]+Vlist[x[1]])==1]
sage: E = Set([Set(s) for s in E])
sage: E = [tuple(s) for s in E]
sage: Gamma = Graph(E)
sage: Gamma
Graph on 8 vertices
sage:
sage: VG = Gamma.vertices()
sage: L1 = []
sage: L2 = []
sage: for v1 in VG:
....: for v2 in VG:
....: N1 = Gamma.neighbors(v1)
....: N2 = Gamma.neighbors(v2)
....: if v1 in N2:
....: L1 = L1+[len([x for x in N1 if x in N2])]
....: if not(v1 in N2) and v1!=v2:
....: L2 = L2+[len([x for x in N1 if x in N2])]
....:
sage: L1; L2
[2, 0, 2, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 2, 2, 0, 0, 2, 2, 2, 2, 0, 2, 2, 2, 0, 2, 2, 2, 2, 0, 2]
[2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2]
This implies that the graph is not strongly regular, therefore f is not bent.
sage: Gamma.spectrum()
[4, 2, 0, 0, 0, -2, -2, -2]
sage:
sage: Gamma.is_bipartite()
False
sage: Gamma.is_hamiltonian()
True
sage: Gamma.is_planar()
False
sage: Gamma.is_regular()
True
sage: Gamma.is_eulerian()
True
sage: Gamma.is_connected()
True
sage: Gamma.is_triangle_free()
False
sage: Gamma.diameter()
2
sage: Gamma.degree_sequence()
[4, 4, 4, 4, 4, 4, 4, 4]
sage: H = matrix(QQ, 8, 8, [(-1)^(Vlist[x[0]]).dot_product(Vlist[x[1]]) for x in C])
sage: H
[ 1 1 1 1 1 1 1 1]
[ 1 -1 1 -1 1 -1 1 -1]
[ 1 1 -1 -1 1 1 -1 -1]
[ 1 -1 -1 1 1 -1 -1 1]
[ 1 1 1 1 -1 -1 -1 -1]
[ 1 -1 1 -1 -1 1 -1 1]
[ 1 1 -1 -1 -1 -1 1 1]
[ 1 -1 -1 1 -1 1 1 -1]
sage: flist = vector(QQ, [int(f(v)) for v in V])
sage: H*flist
(4, 0, 0, 0, -2, -2, -2, 2)
sage: Gamma.spectrum()
[4, 2, 0, 0, 0, -2, -2, -2]
sage: A = matrix(QQ, 8, 8, [f(Vlist[x[0]]+Vlist[x[1]]) for x in C])
sage: A.eigenvalues()
[4, 2, 0, 0, 0, -2, -2, -2]
sage: show(Gamma)
# bent-fcns-cayley-graphs2.png
Here is the picture:

REFERENCES:
[1] Pantelimon Stanica, Graph eigenvalues and Walsh spectrum of Boolean functions, INTEGERS 7(2) (2007), #A32.
[2] Anna Bernasconi, Mathematical techniques for the analysis of Boolean functions, Ph. D. dissertation TD-2/98, Universit di Pisa-Udine, 1998.
[3] Anna Bernasconi and Bruno Codenotti, Spectral Analysis of Boolean Functions as a Graph Eigenvalue Problem, IEEE TRANSACTIONS ON COMPUTERS, VOL. 48, NO. 3, MARCH 1999.
[4] A. Bernasconi, B. Codenotti, J.M. VanderKam. A Characterization of Bent Functions in terms of Strongly Regular Graphs, IEEE Transactions on Computers, 50:9 (2001), 984-985.
[5] Michel Mitton, Minimal polynomial of Cayley graph adjacency matrix for Boolean functions, preprint, 2007.
[6] ——, On the Walsh-Fourier analysis of Boolean functions, preprint, 2006.
of index
.
which is to be transmitted.
,
, where
,
, the errors
and
being, of course, elements of the finite field
. If
(resp.,
) is correctly transmitted then the error
(resp.,
) vanishes, and
(resp.,
).
errors, all of which affect the
(the
being supposed correctly transmitted).
of the
, the errors being
,
. Since the
have been correctly transmitted, the mutilated message can not be in check unless
. Hence the message will fail to check, and the presence of error will be disclosed, unless the
errors
satisfy the system of equations
, of which the determinant is
, so that $\Delta \not=0$. It follows, by Lemma 1, that the system (S) has no solution other than
, for
. Hence
errors, confined to the
, can not escape disclosure if the reference matrix
is of index
. By the same argument, applied a fortiori, a set of less than
errors, confined to the
, will certainly be disclosed when
is of index
.
is of index
, we can make the following statement:
is transmitted with errors not affecting the
, and not more than
in number, the presence of error will infallibly be disclosed.
is of index
.






You must be logged in to post a comment.